简介

在R2中标准基的图示。红蓝向量是这个基的元素。线性代数 A = {\displaystyle \mathbf {A} ={\begin{bmatrix}1&2\\3&4\end{bmatrix}}} 向量 · 向量空间  · 行列式  · 矩阵向量标量 · 向量 · 向量空间 · 向量投影 · 外积（向量积） · 内积（数量积）矩阵与行列式矩阵 · 行列式 · 线性方程组 · 秩 · 核 · 迹 · 单位矩阵 · 初等矩阵 · 方块矩阵 · 分块矩阵 · 三角矩阵 · 非奇异方阵 · 转置矩阵 · 逆矩阵 · 对角矩阵 · 可对角化矩阵 · 对称矩阵 · 反对称矩阵 · 正交矩阵 · 幺正矩阵 · 埃尔米特矩阵 · 反埃尔米特矩阵 · 正规矩阵 · 伴随矩阵 · 余因子矩阵 · 共轭转置 · 正定矩阵 · 幂零矩阵 · 矩阵分解 （LU分解 · 奇异值分解 · QR分解 · 极分解 · 特征分解） · 子式和余子式 · 拉普拉斯展开 · 克罗内克积线性空间与线性变换线性空间 · 线性变换 · 线性子空间 · 线性生成空间 · 基 · 线性映射 · 线性投影 · 线性无关 · 线性组合 · 线性泛函 · 行空间与列空间 · 对偶空间 · 正交 · 特征向量 · 最小二乘法 · 格拉姆-施密特正交化查论编在线性代数中，基（英文：basis，又称基底) 是向量空间里某一群特殊的向量（称为基向量），使得向量空间中的任意向量，都可以唯一地表示成基向量的线性组合（或线性组合的极限）。通过基底可以直接地描述向量空间 V {\displaystyle \mathrm {V} } 上定义的线性映射 f {\displaystyle f} ，因为掌握 f {\displaystyle f} 作用在 V {\displaystyle \mathrm {V} } 的一组基 B {\displaystyle {\mathfrak {B}}} 上的效果，就可以透过 B {\displaystyle {\mathfrak {B}}} 的线性组合得到 f {\displaystyle f} 作用在 V {\displaystyle \mathrm {V} } 中任意向量的效果。

定义

为了记号表示方便，这里仿造数列级数定义一个*向量序列的级数*：

对于向量序列 ${\displaystyle {\{v_i\in <!--\; \in \; -->V\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ ，根据*论和数学归纳法，存在一个向量序列 ${\displaystyle {\{s_i\in <!--\; \in \; -->V\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ 满足

${\displaystyle s_0=v_0}$

对所有的 ${\displaystyle i\in <!--\; \in \; -->\mathbb{N}}$ 有 ${\displaystyle s_{i+1}=s_i+v_i}$

${\displaystyle {\left\{s_i\right\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ 称为 ${\displaystyle {\left\{v_i\right\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ 的级数，通常会仿造数列级数而把 ${\displaystyle s_i}$ 写为

${\displaystyle \underset{k=0}{\overset{i}{\sum <!--\; \sum \; -->}}{v}_k}$

或更直观的

${\displaystyle v_0+v_1+\cdots <!--\; \cdots \; -->+v_i}$

Hamel基

${\displaystyle \mathrm{V}}$ 是定义在域 ${\displaystyle K}$（也就是标量的母空间，如实数系 ${\displaystyle \mathbb{R}}$ 或复数系 ${\displaystyle \mathbb{C}}$）上的向量空间，如果 ${\displaystyle \mathrm{V}}$ 的子集 ${\displaystyle \mathfrak{B}}$ 满足：

${\displaystyle 0_V\notin <!--\; \notin \; -->\mathfrak{B}}$ （也就是零向量不会在 ${\displaystyle \mathfrak{B}}$ 里）

若 ${\displaystyle v\in <!--\; \in \; -->\mathrm{V}}$ 且 ${\displaystyle v\ne <!--\; \ne \; -->0_V}$，则存在唯一的一组相异向量 ${\displaystyle e_1,e_2,\dots <!--\; \dots \; -->,e_n\in <!--\; \in \; -->\mathfrak{B}}$ 和唯一的一组标量 ${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1,{\mathrm{\lambda <!--\; \lambda \; -->}}_2,\dots <!--\; \dots \; -->,{\mathrm{\lambda <!--\; \lambda \; -->}}_n\in <!--\; \in \; -->K}$ 使得 ${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1\cdot <!--\; \cdot \; -->e_1+{\mathrm{\lambda <!--\; \lambda \; -->}}_2\cdot <!--\; \cdot \; -->e_2+\cdots <!--\; \cdots \; -->+{\mathrm{\lambda <!--\; \lambda \; -->}}_n\cdot <!--\; \cdot \; -->e_n=v}$ 。

则称 ${\displaystyle \mathfrak{B}}$ 是向量空间 ${\displaystyle \mathrm{V}}$ 的一组Hamel基。${\displaystyle \mathfrak{B}}$ 里的元素被称为基向量 ，若基向量的总数是有限个，${\displaystyle \mathfrak{B}}$ 则会被称为有限基或直接简称为基。

上面的第二个条件，也可以等价地改写为以下两条：

线性无关(linear independence)对任意相异的${\displaystyle e_1,e_2,\dots <!--\; \dots \; -->,e_n\in <!--\; \in \; -->\mathfrak{B}}$ 和任意的 ${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1,{\mathrm{\lambda <!--\; \lambda \; -->}}_2,\dots <!--\; \dots \; -->,{\mathrm{\lambda <!--\; \lambda \; -->}}_n\in <!--\; \in \; -->K}$，若 ${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1\cdot <!--\; \cdot \; -->e_1+{\mathrm{\lambda <!--\; \lambda \; -->}}_2\cdot <!--\; \cdot \; -->e_2+\cdots <!--\; \cdots \; -->+{\mathrm{\lambda <!--\; \lambda \; -->}}_n\cdot <!--\; \cdot \; -->e_n=0_V}$，则${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1={\mathrm{\lambda <!--\; \lambda \; -->}}_2=\dots <!--\; \dots \; -->={\mathrm{\lambda <!--\; \lambda \; -->}}_n=0_K}$生成律(spanning property)对任意${\displaystyle v\in <!--\; \in \; -->\mathrm{V}}$，存在相异向量 ${\displaystyle e_1,e_2,\dots <!--\; \dots \; -->,e_n\in <!--\; \in \; -->\mathfrak{B}}$和 ${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1,{\mathrm{\lambda <!--\; \lambda \; -->}}_2,\dots <!--\; \dots \; -->,{\mathrm{\lambda <!--\; \lambda \; -->}}_n\in <!--\; \in \; -->K}$ 使得 ${\displaystyle {\mathrm{\lambda <!--\; \lambda \; -->}}_1{e}_1+{\mathrm{\lambda <!--\; \lambda \; -->}}_2{e}_2+\cdots <!--\; \cdots \; -->+{\mathrm{\lambda <!--\; \lambda \; -->}}_n{e}_n=v}$

等价性来自于线性无关：

若有第二组相异 ${\displaystyle E_1,E_2,\dots <!--\; \dots \; -->,E_m\in <!--\; \in \; -->\mathfrak{B}}$ 基向量和第二组标量 ${\displaystyle c_1,c_2,\dots <!--\; \dots \; -->,c_m\in <!--\; \in \; -->K}$ 也满足 ${\displaystyle c_1\cdot <!--\; \cdot \; -->E_1+c_2\cdot <!--\; \cdot \; -->E_2+\cdots <!--\; \cdots \; -->+c_m\cdot <!--\; \cdot \; -->E_m=v}$ 的话，把这住两组基向量合并，并重新排列，于两组间重复的记为 ${\displaystyle w_1,w_2,\dots <!--\; \dots \; -->,w_l\in <!--\; \in \; -->\mathfrak{B}}$ ，其他不重复的部分，第一组的记为 ${\displaystyle v_1,v_2,\dots <!--\; \dots \; -->,v_{n-<!--\; -\; -->l}\in <!--\; \in \; -->\mathfrak{B}}$ ；而第二组的记为 ${\displaystyle u_1,u_2,\dots <!--\; \dots \; -->,u_{m-<!--\; -\; -->l}\in <!--\; \in \; -->\mathfrak{B}}$ ；然后设 ${\displaystyle w_1,w_2,\dots <!--\; \dots \; -->,w_l\in <!--\; \in \; -->\mathfrak{B}}$ 于原来第一组对应的标量系数是 ${\displaystyle {\mathrm{\alpha <!--\; \alpha \; -->}}_1,{\mathrm{\alpha <!--\; \alpha \; -->}}_2,\dots <!--\; \dots \; -->,{\mathrm{\alpha <!--\; \alpha \; -->}}_l\in <!--\; \in \; -->K}$ ；原第二组则是对应 ${\displaystyle a_1,a_2,\dots <!--\; \dots \; -->,a_l\in <!--\; \in \; -->K}$ 。另外 ${\displaystyle v_1,v_2,\dots <!--\; \dots \; -->,v_{n-<!--\; -\; -->l}\in <!--\; \in \; -->\mathfrak{B}}$ 对应的标量系数则为 ${\displaystyle {\mathrm{\beta <!--\; \beta \; -->}}_1,{\mathrm{\beta <!--\; \beta \; -->}}_2,\dots <!--\; \dots \; -->,{\mathrm{\beta <!--\; \beta \; -->}}_{n-<!--\; -\; -->l}\in <!--\; \in \; -->K}$ ；${\displaystyle u_1,u_2,\dots <!--\; \dots \; -->,u_{m-<!--\; -\; -->l}\in <!--\; \in \; -->\mathfrak{B}}$ 对应的标量系数则为 ${\displaystyle b_1,b_2,\dots <!--\; \dots \; -->,b_{m-<!--\; -\; -->l}\in <!--\; \in \; -->K}$ ； 这样把 ${\displaystyle v\in <!--\; \in \; -->\mathrm{V}}$ 的第一组线性组合表达式减去第二组会有

${\displaystyle \underset{i=1}{\overset{l}{\sum <!--\; \sum \; -->}}({\mathrm{\alpha <!--\; \alpha \; -->}}_i-<!--\; -\; -->a_i)\cdot <!--\; \cdot \; -->w_i+\underset{j=1}{\overset{n-<!--\; -\; -->l}{\sum <!--\; \sum \; -->}}{\mathrm{\beta <!--\; \beta \; -->}}_j\cdot <!--\; \cdot \; -->v_j+\underset{k=1}{\overset{m-<!--\; -\; -->l}{\sum <!--\; \sum \; -->}}(-<!--\; -\; -->b_k)\cdot <!--\; \cdot \; -->u_k=0_V}$

这样依据线性无关，就有

${\displaystyle {\mathrm{\alpha <!--\; \alpha \; -->}}_1-<!--\; -\; -->a_1={\mathrm{\alpha <!--\; \alpha \; -->}}_2-<!--\; -\; -->a_2=\cdots <!--\; \cdots \; -->={\mathrm{\alpha <!--\; \alpha \; -->}}_l-<!--\; -\; -->a_l=0_K}$${\displaystyle {\mathrm{\beta <!--\; \beta \; -->}}_1={\mathrm{\beta <!--\; \beta \; -->}}_2=\cdots <!--\; \cdots \; -->={\mathrm{\beta <!--\; \beta \; -->}}_{n-<!--\; -\; -->l}=0_K}$${\displaystyle b_1=b_2=\cdots <!--\; \cdots \; -->=b_{m-<!--\; -\; -->l}=0_K}$

这就确保任意 ${\displaystyle v\in <!--\; \in \; -->\mathrm{V}}$ 的线性组合表达式都是用同一组的基向量，且其标量系数也是唯一的。

Schauder基

除了上小节单以线性组合定义的Hamel基，也有以无穷级数展开任意向量为动机来定义基。

${\displaystyle \mathrm{V}}$ 是定义在域 ${\displaystyle K}$ 上的巴拿赫空间（范数记为 ${\displaystyle \Vert <!--\; \Vert \; -->v\Vert <!--\; \Vert \; -->}$ ），若向量序列 ${\displaystyle {\{e_i\in <!--\; \in \; -->V\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ 满足：

对所有自然数 ${\displaystyle i\in <!--\; \in \; -->\mathbb{N}}$ ，${\displaystyle e_i\ne <!--\; \ne \; -->0_V}$ （也就是零向量不会在 ${\displaystyle {\{e_i\in <!--\; \in \; -->V\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ 里）

对每个 ${\displaystyle v\in <!--\; \in \; -->\mathrm{V}}$ ，都存在唯一组标量${\displaystyle {\{{\mathrm{\lambda <!--\; \lambda \; -->}}_i\in <!--\; \in \; -->K\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$，使得对所有的 ，存在 ${\displaystyle m\in <!--\; \in \; -->{\mathbb{Z}}^{+}}$ 使得 ${\displaystyle n\in <!--\; \in \; -->\mathbb{N}}$ 且 则 （仿造数列极限而定义）

那向量序列 ${\displaystyle {\{e_i\in <!--\; \in \; -->V\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$ 则被称为是向量空间 ${\displaystyle \mathrm{V}}$ 的一组Schauder基。

第二项条件通常会简写为

对每个 ${\displaystyle v\in <!--\; \in \; -->\mathrm{V}}$ ，都存在唯一组标量${\displaystyle {\{{\mathrm{\lambda <!--\; \lambda \; -->}}_i\in <!--\; \in \; -->K\}}_{i\in <!--\; \in \; -->\mathbb{N}}}$，使 ${\displaystyle v=\underset{n\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}\underset{i=0}{\overset{n}{\sum <!--\; \sum \; -->}}{\mathrm{\lambda <!--\; \lambda \; -->}}_i\cdot <!--\; \cdot \; -->e_i}$

甚至写为

${\displaystyle v=\underset{i=0}{\overset{\mathrm{\infty <!--\; \infty \; -->}}{\sum <!--\; \sum \; -->}}{\mathrm{\lambda <!--\; \lambda \; -->}}_i\cdot <!--\; \cdot \; -->e_i}$

例子

在傅立叶级数的研究中，函数${\displaystyle \{1\}\cup <!--\; \cup \; -->\{\sin <!--\; \; -->(nx),\cos <!--\; \; -->(nx)|n\in <!--\; \in \; -->\mathbb{N}\}}$是所有的在区间上为平方可积分的（实数或复数值）的函数的（实数或复数）向量空间的“正交基”，这种函数${\displaystyle f(x)}$满足

函数族${\displaystyle \{1\}\cup <!--\; \cup \; -->\{\sin <!--\; \; -->(nx),\cos <!--\; \; -->(nx)|n\in <!--\; \in \; -->\mathbb{N}\}}$是线性无关的，所有在上平方可积分的函数是它们的“无限线性组合”，在如下意义上

${\displaystyle \underset{n\to <!--\; \to \; -->\mathrm{\infty <!--\; \infty \; -->}}{lim}{\int <!--\; \int \; -->}_0^{2\mathrm{\pi <!--\; \pi \; -->}}|a_0+\underset{k=1}{\overset{n}{\sum <!--\; \sum \; -->}}(a_k\cos <!--\; \; -->(kx)+b_k\sin <!--\; \; -->(kx))-<!--\; -\; -->f(x){|}^{2}dx=0}$

对于适合的（实数或复数）系数ak, bk。但是多数平方可积分函数不能表达为这些基函数的有限线性组合，因为它们不构成Hamel基。这个空间的所有Hamel基都大于这个函数的只可数无限*。此类空间的Hamel基没有什么价值，而这些空间的正交基是傅立叶分析的根本。

维度

如果基中元素个数有限，就称向量空间为有限维向量空间，将元素的个数称作向量空间的维数。

事实上，不是所有空间都拥有由有限个元素构成的基底。这样的空间称为无限维空间。某些无限维空间上可以定义由无限个元素构成的基。在现代*论中，如果承认选择公理，就可以证明任何向量空间都拥有一组基。一个向量空间的基不止一组，但同一个空间的两组不同的基，它们的元素个数或势（当元素个数是无限的时候）会是相等的。一组基里面的任意一部分向量都是线性无关的；反之，如果向量空间拥有一组基，那么在向量空间中取一组线性无关的向量，一定能得到一组基。特别地，在内积向量空间中，可以定义正交的概念。通过特别的*，可以将任意的一组基变换成正交基乃至标准正交基。

性质

设${\displaystyle \mathfrak{B}}$是向量空间${\displaystyle \mathrm{V}}$的子集。则${\displaystyle \mathfrak{B}}$是基，当且仅当满足了下列任一条件：

${\displaystyle \mathrm{V}}$是${\displaystyle \mathfrak{B}}$的极小生成集，就是说只有${\displaystyle \mathfrak{B}}$能生成${\displaystyle \mathrm{V}}$，而它的任何真子集都不能生成全部的向量空间。

${\displaystyle \mathfrak{B}}$是${\displaystyle \mathrm{V}}$中线性无关向量的极大*，就是说${\displaystyle \mathfrak{B}}$在${\displaystyle \mathrm{V}}$中是线性无关(线性独立)*，而且${\displaystyle \mathrm{V}}$中没有其他线性无关(线性独立)*包含它作为真子集。

${\displaystyle \mathrm{V}}$中所有的向量都可以按唯一的方式表达为${\displaystyle \mathfrak{B}}$中向量的线性组合。如果基是有序的，则在这个线性组合中的系数提供了这个向量关于这个基的坐标。

如果承认良序定理或任何选择公理的等价物，那么作为推论，可以证明任何的向量空间都拥有一组基。（证明：良序排序这个向量空间的元素。建立不线性依赖于前面元素的所有元素的子集。它就是基）。反过来也是真的。一个向量空间的所有基都拥有同样的势（元素个数），叫做这个向量空间的维度。这个结果叫做维度定理，它要求系统承认严格弱形式的选择公理即超滤子引理。

例子

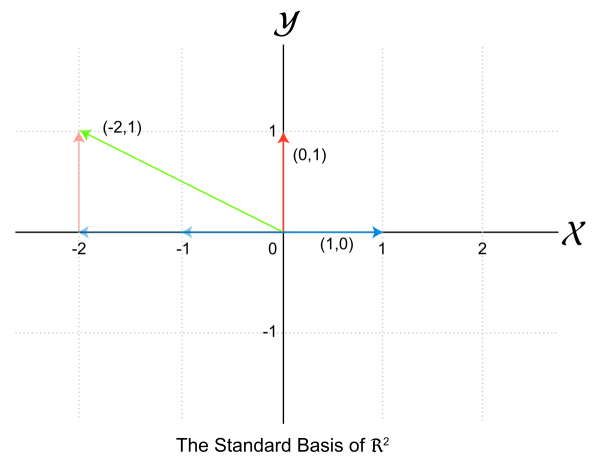
考虑所有坐标 (a, b)的向量空间R2，这里的a和b都是实数。则非常自然和简单的基就是向量e1 = (1,0)和e2 = (0,1):假设v = (a, b)是R2中的向量，则v = a (1,0) + b(0,1)。而任何两个线性无关向量如 (1,1)和(−1,2)，也形成R2的一个基。

更一般的说，给定自然数n。n个线性无关的向量e1, e2, ..., en可以在实数域上生成Rn。因此，它们也是的一个基而Rn的维度是n。这个基叫做Rn的标准基。

设V是由函数et和e2t生成的实数向量空间。这两个函数是线性无关的，所有它们形成了V的基。

设R指示所有实数多项式的向量空间；则 (1, x, x2, ...)是R的基。R的维度的势因此等于${\displaystyle {\mathrm{\aleph <!--\; \aleph \; -->}}_0}$.

标准基

在行向量空间${\displaystyle {\mathbb{R}}^n}$中有单位行向量

${\displaystyle E_{(1)}=(1,0,...,0),E_{(2)}=(0,1,...,0),...,E_{(n)}=(0,0,...,1)}$

那么在该空间中，任意向量${\displaystyle X=(x_1,x_2,...,x_n)}$,都可以唯一表示成${\displaystyle X=x_1{E}_{(1)}+x_2{E}_{(2)}+...+x_n{E}_{(n)}}$.然后我们可以看出，${\displaystyle {\mathbb{R}}^n}$可以由它的向量子空间构成

${\displaystyle {\mathbb{R}}^n}$.

同样的，单位列向量就可以表达为${\displaystyle {\mathbb{R}}^n}$${\displaystyle =}$.

线性无关的单位行向量${\displaystyle E_{(1)},E_{(2)},...,E_{(n)}}$生成${\displaystyle {\mathbb{R}}^n}$. 那么${\displaystyle E_{(1)},E_{(2)},...,E_{(n)}}$是${\displaystyle {\mathbb{R}}^n}$的基，称这个基为标准基.

基的扩张

如上所述，一个向量空间的每一组基都是一个极大的线性无关*，同时也是极小的生成*。可以证明，如果向量空间拥有一组基，那么每个线性无关的子集都可以扩张成一组基（也称为基的扩充定理），每个能够生成整个空间的子集也必然包含一组基。特别地，在任何线性无关*和任何生成*之间有一组基。以数学语言来说：如果${\displaystyle \mathfrak{L}}$是在向量空间${\displaystyle \mathrm{V}}$中的一个线性无关*而*${\displaystyle \mathfrak{G}}$是一个包含${\displaystyle \mathfrak{L}}$而且能够生成${\displaystyle \mathrm{V}}$的*，则存在${\displaystyle \mathrm{V}}$的一组基${\displaystyle \mathfrak{B}}$，它包含了${\displaystyle \mathfrak{L}}$而且是${\displaystyle \mathfrak{G}}$的子集：${\displaystyle \mathfrak{L}\subseteq <!--\; \subseteq \; -->\mathfrak{B}\subseteq <!--\; \subseteq \; -->\mathfrak{G}}$。

以上两个结论可以帮助证明一个*是否是给定向量空间的基。如果不知道某个向量空间的维度，证明一个*是它的基需要证明这个*不仅是线性无关的，而且能够生成整个空间。如果已知这个向量空间的维度（有限维），那么这个*的元素个数必须等于维数，才可能是它的基。在两者相等时，只需要证明这个*线性无关，或这个*能够生成整个空间这两者之一就够了。这是因为线性无关的子集必然能扩充成基；而这个*的元素个数已经等于基的元素个数，需要添加的元素是0个。这说明原*就是一组基。同理，能够生成整个空间的*必然包含一组基作为子集；但假如这个子集是真子集，那幺元素个数必须少于原*的元素个数。然而原*的元素个数等于维数，也就是基的元素个数，这是矛盾的。这说明原*就是一组基。

有序基和坐标

基底是作为向量空间的子集定义的，其中的元素并不按照顺序排列。为了更方便相关的讨论，通常会将基向量进行排列。比如说将：${\displaystyle \mathfrak{B}=\{e_1,e_2,\cdots <!--\; \cdots \; -->,e_n\}}$写成有序向量组：${\displaystyle (e_1,e_2,\cdots <!--\; \cdots \; -->,e_n)}$。这样的有序向量组称为有序基。在有限维向量空间和可数维数的向量空间中，都可以自然地将基底表示成有序基。在有序基下，任意的向量都可以用确定的数组表示，称为向量的坐标。例如，在使用向量的坐标表示的时候习惯谈论“第一个”或“第二个”坐标，这只在指定了基的次序前提下有意义。在这个意义下，有序基可以看作是向量空间的坐标架。

设${\displaystyle \mathrm{V}}$是在域${\displaystyle \mathbb{F}}$上的n维向量空间。在${\displaystyle \mathrm{V}}$上确定一个有序基等价于确定一个从坐标空间${\displaystyle {\mathbb{F}}^n}$到${\displaystyle \mathrm{V}}$的一个选定线性同构${\displaystyle \mathrm{\varphi <!--\; \varphi \; -->}}$。

证明：这个证明利用了${\displaystyle {\mathbb{F}}^n}$的标准基是有序基的事实。

首先假设

${\displaystyle \mathrm{\varphi <!--\; \varphi \; -->}:{\mathbb{F}}^n\to <!--\; \to \; -->\mathrm{V}}$是线性同构。可以定义${\displaystyle \mathrm{V}}$的一组有序基${\displaystyle \{v_i{\}}_{1⩽<!--\; ⩽\; -->i⩽<!--\; ⩽\; -->n}}$如下：${\displaystyle v_i=\mathrm{\varphi <!--\; \varphi \; -->}(e_i),\mathrm{\forall <!--\; \forall \; -->}i,1⩽<!--\; ⩽\; -->i⩽<!--\; ⩽\; -->n.}$

其中的${\displaystyle \{e_i{\}}_{1⩽<!--\; ⩽\; -->i⩽<!--\; ⩽\; -->n}}$是${\displaystyle {\mathbb{F}}^n}$的标准基。

反过来说，给定一个有序基，考虑如下定义的映射

φ(x) = x1v1 + x2v2 + ... + xnvn,

这里的x = x1e1 + x2e2 + ... + xnen是Fn的一个元素。不难检查出φ是线性同构。

这两个构造明显互逆。所以V的有序基一一对应于线性同构Fn → V。

确定自有序基{vi}线性映射φ的逆映射为V装备了坐标：如果对于向量v ∈ V, φ-1(v) = (a1, a2,...,an) ∈ Fn，则aj = aj(v)的分量是v的坐标，在v = a1(v) v1 + a2(v) v2 + ... + an(v) vn的意义上。

从向量v到分量aj(v)的映射是从V到F的线性映射，因为φ-1是线性的。所以它们是线性泛函。它们形成V的对偶空间的基，叫做对偶基。